퀵 정렬
Quick(빠른) + Sort(정렬)
퀵 정렬은 가장 빠른 정렬 알고리즘으로 잘 알려져 있습니다.
퀵 정렬은 데이터 그룹에서 그룹을 나누는 기준인 피벗(pivot)을 선택하고, 피벗을 기준으로 그룹을 나누는 것을 반복하여 각 그룹이 1개가 되면 정렬을 마칩니다.
아래의 그림을 통해 자세하게 살펴보겠습니다.
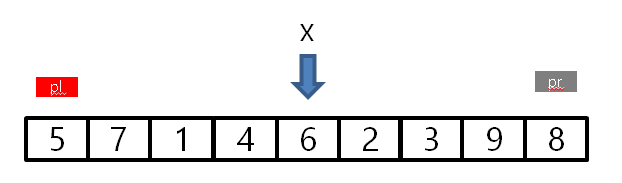
왼쪽 끝에 커서를 pl, 오른쪽 끝의 커서를 pr, 중간의 x 화살표를 피벗이라고 하겠습니다.
양쪽 끝의 커서는 피벗과 비교할 숫자를 가리키게 됩니다.
- [pl] >= x 가 성립하는 데이터를 찾을 때까지 pl을 오른쪽으로 스캔합니다.
- [pr] <= x 가 성립하는 데이터를 찾을 때까지 pr을 왼쪽으로 스캔합니다.
위의 과정을 거치게 되면 커서의 위치가 아래와 같이 바뀌게 됩니다.
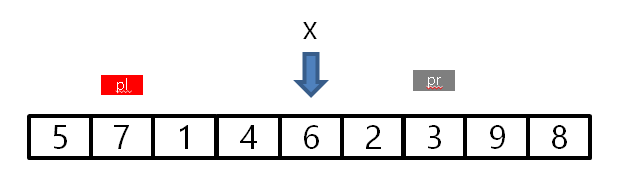
여기서 pl의 데이터인 7과 오른쪽의 데이터 3의 위치를 변경하고 다시 스캔을 시작합니다.
다시 스캔을 진행하면 커서의 위치는 6과 2에서 멈춥니다.

마지막으로 6과 2의 위치를 변경합니다.

첫 번째 정렬의 과정을 마치게 되면
데이터 그룹을 피벗(6)을 기준으로 두 개의 그룹으로 나눌수 있습니다.
- 5, 3, 1, 4, 2
- 7, 9, 8
두개의 그룹에서 위의 정렬을 과정을 마지막까지 거치고 나누어진 그룹이 1개가 될 때 정렬은 끝나게 됩니다.
위의 예시에서는 두 개의 커서의 값이 피벗과 일치하는 값이 만들어지지 않았지만, 왼쪽의 pl과 오른쪽의 pr의 값이 같은 값을 가르키게 될때는 그냥 동일한 요소 두개의 교환합니다.
만약 교환하지 않는다면 pl과 pr이 동일한 위치에 존재하는지 검사를 해야 합니다.(비용이 더 많이 들 수 있습니다.)
아래는 배열을 이용한 퀵 정렬 메서드입니다.
package quicksort;
public class QuickSort {
// 배열(data)의 요소 data[pl]과 data[pr] 교환
static void swap(int[] data, int pl, int pr) {
int temp = data[pl];
data[pl] = data[pr];
data[pr] = temp;
}
static void quickSort(int[] data, int left, int right) { // left, right는 각 커서의 시작점
int pl = left;
int pr = right;
int pivot = data[(pl + pr) / 2]; // 피벗은 각 끝의 커서의 중간 값으로 선택
do {
while (data[pl] < pivot) { // data[pl] 값이 pivot보다 큰 수 탐색
pl++;
}
while (data[pr] > pivot) { // data[pr] 값이 pivot보다 작은 수 탐색
pr--;
}
if (pl <= pr) { // pl보다 pr이 크면 교환(오름차순)
swap(data, pl++, pr--);
}
} while (pl <= pr);
// 정렬 끝난 후 나누어진 두개의 그룹에 데이터 수를 체크
if (left < pr)
quickSort(data, left, pr); // left가 pr보다 작으면 그룹의 수가 1개 이상이기 때문에 다시 정렬
if (pl < right)
quickSort(data, pl, right); // pl이 right보다 작으면 그룹의 수가 1개 이상이기 때문에 다시 정렬
}
public static void main(String[] args) {
int[] x = { 5, 7, 1, 4, 6, 2, 3, 9, 8 };
quickSort(x, 0, x.length - 1);
for(int i = 0 ; i < x.length ; i++) {
System.out.println(x[i]);
}
}
}
2021.12.31 - [Algorithm/Baekjoon] - [백준 알고리즘][자바] 2798번 : 블랙잭 & 브루트 포스(Brute Force)
[백준 알고리즘][자바] 2798번 : 블랙잭 & 브루트 포스(Brute Force)
브루트 포스 알고리즘의 개념 중의 하나로 영어의 뜻은 다음과 같습니다. Brute : 난폭한 + Force (힘) 이러한 뜻을 내포하고 있는 이유는 브루트 포스의 알고리즘은 정답으로 도출될 수 있는 모든
hyunipad.tistory.com
백준 알고리즘 2798번에서는 브루트 포스를 이용하여 모든 경우의 수를 탐색해야 했지만, 퀵 정렬을 이용하여 데이터를 선형화 시키면 검사해야 할 경우의 수를 줄일 수 있습니다.
아래는 위의 포스팅에서 풀었던 코드에 퀵 정렬을 추가한 예시입니다.
백준에서 컴파일해보니 시간에서 많은 차이가 보이진 않지만... 경우의 수가 많아질수록 차이를 보일 수 있겠습니다.
그렇지 않더라도 알고 있는 게 중요하죠..ㅎㅎ
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
public class Main {
public static void main(String[] args) throws NumberFormatException, IOException {
// 백준 알고리즘 2798번
// 카지노에서 제일 인기 있는 게임 블랙잭의 규칙은 상당히 쉽다. 카드의 합이 21을 넘지 않는 한도 내에서, 카드의 합을 최대한 크게 만드는 게임이다. 블랙잭은 카지노마다 다양한 규정이 있다.
//
// 한국 최고의 블랙잭 고수 김정인은 새로운 블랙잭 규칙을 만들어 상근, 창영이와 게임하려고 한다.
//
// 김정인 버전의 블랙잭에서 각 카드에는 양의 정수가 쓰여 있다. 그 다음, 딜러는 N장의 카드를 모두 숫자가 보이도록 바닥에 놓는다. 그런 후에 딜러는 숫자 M을 크게 외친다.
//
// 이제 플레이어는 제한된 시간 안에 N장의 카드 중에서 3장의 카드를 골라야 한다. 블랙잭 변형 게임이기 때문에, 플레이어가 고른 카드의 합은 M을 넘지 않으면서 M과 최대한 가깝게 만들어야 한다.
//
// N장의 카드에 써져 있는 숫자가 주어졌을 때, M을 넘지 않으면서 M에 최대한 가까운 카드 3장의 합을 구해 출력하시오.
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String[] NM = br.readLine().split(" ");
String[] nums_str = br.readLine().split(" ");
int N = Integer.parseInt(NM[0]); // 카드의 개수
int M = Integer.parseInt(NM[1]); // 카드의 합 목표
int[] nums = new int[N]; // 카드의 숫자들
for (int i = 0; i < N; i++) {
nums[i] = Integer.parseInt(nums_str[i]);
}
quickSort(nums, 0, N -1);
int answer = search(nums, N, M);
bw.write(String.valueOf(answer));
br.close();
bw.flush();
bw.close();
}
// 탐색
static int search(int[] nums, int N, int M) {
int result = 0;
for (int i = 0; i < N - 2; i++) {
for (int j = i + 1; j < N - 1; j++) {
for (int k = j + 1; k < N; k++) {
int answer = nums[i] + nums[j] + nums[k];
if(i == j-1 && i == k-2 && answer > M) {
return result;
}
if (M == answer) {
return answer;
}
if (result < answer && answer < M) {
result = answer;
}
}
}
}
return result;
}
// 배열(data)의 요소 data[pl]과 data[pr] 교환
static void swap(int[] data, int pl, int pr) {
int temp = data[pl];
data[pl] = data[pr];
data[pr] = temp;
}
static void quickSort(int[] data, int left, int right) { // left, right는 각 커서의 시작점
int pl = left;
int pr = right;
int pivot = data[(pl + pr) / 2]; // 피벗은 각 끝의 커서의 중간 값으로 선택
do {
while (data[pl] < pivot) { // data[pl] 값이 pivot보다 큰 수 탐색
pl++;
}
while (data[pr] > pivot) { // data[pr] 값이 pivot보다 작은 수 탐색
pr--;
}
if (pl <= pr) { // pl보다 pr이 크면 교환(오름차순)
swap(data, pl++, pr--);
}
} while (pl <= pr);
// 정렬 끝난 후 나누어진 두개의 그룹에 데이터 수를 체크
if (left < pr)
quickSort(data, left, pr); // left가 pr보다 작으면 그룹의 수가 1개 이상이기 때문에 다시 정렬
if (pl < right)
quickSort(data, pl, right); // pl이 right보다 작으면 그룹의 수가 1개 이상이기 때문에 다시 정렬
}
}
퀵 정렬을 구현하는 방법 중 스택을 이용한 방법도 존재합니다.
스택을 이용하면 좀 더 다양한 데이터에 대해서 정렬을 할 수 있습니다.
C로는 스택을 다뤄봤지만 자바로는 다뤄보지 않았기 때문에 스택을 먼저 공부한 후에 다시 스택을 이용한 퀵 정렬을 소개해 보도록 하겠습니다.
'Algorithm > Theory' 카테고리의 다른 글
| [자바] 큐(Queue) - 선입선출(FIFO : First In First Out)의 자료구조 (0) | 2022.01.20 |
|---|---|
| [자바] 후입선출(LIFO, Last In First Out)의 자료구조 - 스택(Stack) (0) | 2022.01.09 |
| 자료구조 - 순환 큐(Circular Queue) (0) | 2021.02.27 |
| 자료 구조 - 스택(Stack) (0) | 2021.01.27 |
| 자료 구조 - 더블 링크드 리스트(Double Linked List) (0) | 2021.01.19 |



댓글