반응형
병합 정렬(Merge Sort)은 안정 정렬 중 하나이며, 분할 정복 알고리즘을 사용한 정렬 방법입니다.
분할 정복(divide and conquer)은 하나의 문제를 두 개의 문제로 분리하고 각각 해결한 다음 결과를 모아서 문제를 해결하는 방법입니다.
병합 정렬(Merge Sort)이란?
병합 정렬은 분할 정복 알고리즘에 따라서 하나의 리스트를 두 개의 리스트로 분할한 다음 각각의 분할된 리스트를 정렬한 후에 합하여 정렬된 하나의 리스트로 만드는 방법입니다.
병합 정렬은 아래와 같은 순서로 진행됩니다.
- 분할(Divide) : 입력된 리스트를 두개의 리스트로 분할한다.
- 정복(Conquer) : 분할된 리스트를 정렬한다. 분할된 리스트의 크기가 작지 않다면 재귀 호출을 이용하여 다시 분할 정복합니다.
- 결합(Combine) : 정렬된 두 개의 리스트를 하나의 리스트로 결합한다.
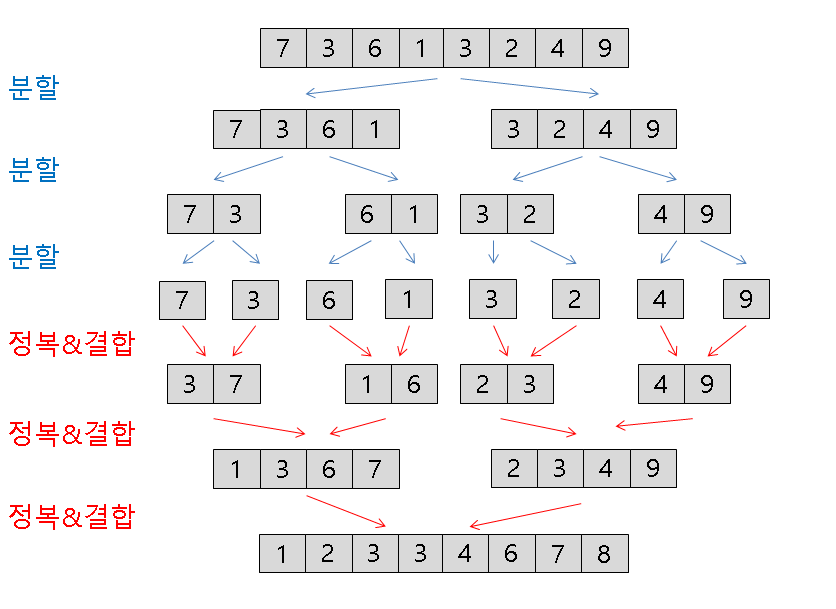
병합 정렬 알고리즘 개념
분할된 리스트를 하나로 다시 합칠 때 정렬을 하면서 합치게 됩니다.
이때 리스트들을 병합하는 과정을 살펴보도록 하겠습니다.
- 두 개의 리스트의 값을 처음부터 비교하여 두 개의 리스트의 값 중에 작은 값을 새로운 리스트로 옮긴다.
- 두 개의 리스트중 하나의 리스트가 끝날 때까지 반복한다.
- 하나의 리스트가 끝나게 되면 남은 리스트의 값을 모두 새로운 리스트로 옮긴다.
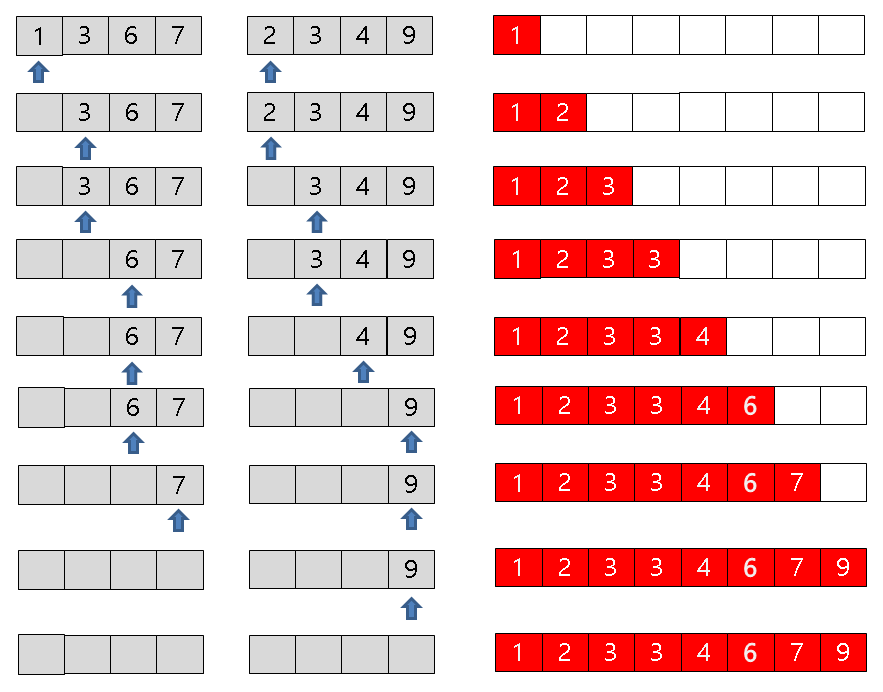
위의 과정을 코드로 살펴보도록 하겠습니다.
public class MergeArray {
static void merge(int[] a, int na, int[] b, int nb, int[] c) {
int pa = 0;
int pb = 0;
int pc = 0;
while(pa < na && pb < nb) {
c[pc++] = (a[pa] <= b[pb]) ? a[pa++] : b[pb++]; // 둘중 작은 값을 c에 저장합니다.
}
while (pa < na) {
c[pc++] = a[pa++]; // a배열에 남은 숫자들을 c에 저장합니다.
}
while (pb < nb) {
c[pc++] = b[pb++]; // b배열에 남은 숫자들을 c에 저장합니다.
}
}
}위의 코드는 a 배열과 b 배열을 병합하여 정렬된 c 배열을 만드는 단순한 알고리즘입니다.
실제 코드에서는 재귀 호출을 통해서 배열을 잘게 쪼갠 후에 나누어진 배열들을 병합 과정을 통해서 합치면서 배열이 정렬되어집니다.
병합 정렬 알고리즘 코드
public class MergeSort {
static int[] buff;
static void merge(int[] a, int left, int right) {
if(left < right) {
int i;
int center = (left + right) / 2;
int p = 0;
int j = 0;
int k = left;
merge(a, left, center); // 재귀 호출을 통해서 앞부분 병합 정렬(잘게 쪼개줌).
merge(a, center + 1, right); // 재귀 호출을 통해서 뒷부분 병합 정렬(잘게 쪼개줌).
for(i = left; i <= center; i++) {
buff[p++] = a[i]; // buff에 center 기준 왼쪽 배열 저장
}
while(i <= right && j < p) { // i = center + 1
a[k++] = (buff[j] <= a[i]) ? buff[j++] : a[i++];
}
while(j < p) { // 나머지 값 복사
a[k++] = buff[j++];
}
}
}
static void mergeSort(int[] a, int n) {
buff = new int[n];
merge(a, 0, n-1);
buff = null;
}
}반응형
'Algorithm > Theory' 카테고리의 다른 글
| 에라토스테네스의 체(백준 1713번 : 골드바흐 파티션) (0) | 2023.12.09 |
|---|---|
| 유클리드 호제법 (1) | 2023.12.03 |
| [Java] Counting Sort(카운팅 정렬) (0) | 2022.05.07 |
| [자바] 셸 정렬(Shell Sort) (0) | 2022.01.27 |
| [자바] 단순 선택 정렬과 단순 삽입 정렬 (0) | 2022.01.22 |




댓글