반응형
오늘은 소수 판별법 중 하나인 에라토스테네스의 체에 대한 리뷰
오늘도 당연히 그림 같은 건 생략한다. 왜냐하면 귀찮기 때문
에라토스테네스의 체는 소수 판별법 중에 하나인데, 특정 숫자 범위 이내의 숫자들 중 소수들을 찾을 때 사용 가능하다.
찾는 법은 아주 간단한데, 예를 들어 100 이하의 소수를 찾으려고 할 때 2의 배수, 3의 배수, 5의 배수, 7의 배수를 제외하면 남은 숫자가 소수이다. 이렇게 걸러내는 방식이 마치 체로 걸러내는 것과 비슷하여 이름이 붙여졌다.
(코드는 아래 주석과 함께)
아래는 에라토스테네스의 체를 사용하는 문제이다.
나는 에라토스테네스의 체를 모르는 채로 아래 문제를 풀었는데, 2의 배수 3의 배수까지 걸러내는 것에는 다가갔는데 그 이후로는 실패하여 검색해서 해결했다.
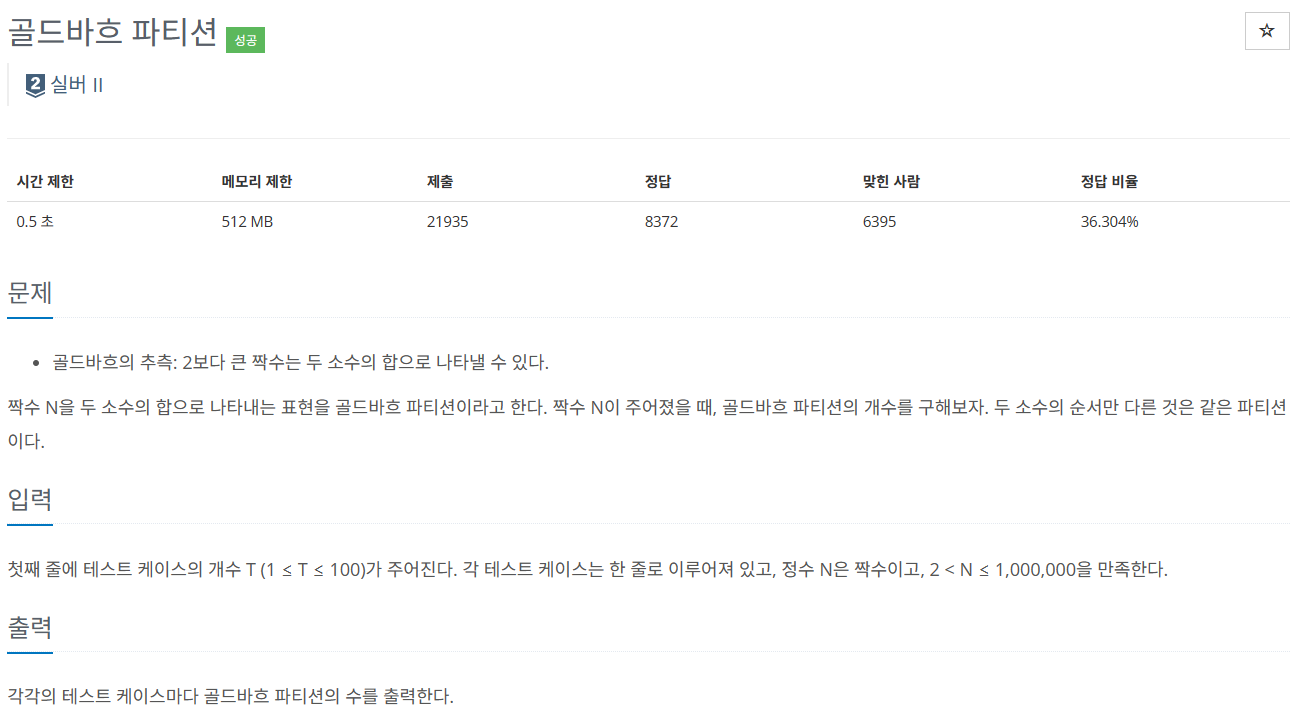
원래 골드바흐의 추측의 정석은
짝수 N보다 작은 소수 중 하나가 A라고 했을 때, N-A도 소수이면 골드바흐 파티션이라고 할 수 있다.
근데 위의 방식으로 해결하려고 하면 소수의 판별을 2번이나 해야 하기 때문에 시간 초과에 걸린다.
따라서 소수를 한 번에 찾은 다음 그 집합에서 A, N-A인 애들을 카운트해줘야 한다.
그 집합들을 구할 때, 에라토스테네스의 체를 사용한다.
아래는 그 코드이다.
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.List;
public class Number_17103 {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
for(int i = 0 ; i < T ; i++) {
int N = Integer.parseInt(br.readLine());
boolean[] isPrime = new boolean[N + 1];
initEratosthenes(isPrime);
getEratosthenes(isPrime);
int result = 0;
for(int i2 = 2; i2 <= isPrime.length / 2; i2++) {
if(isPrime[i2] && isPrime[N - i2]) result++;
}
bw.write(String.valueOf(result) + "\n");
}
bw.flush();
bw.close();
br.close();
}
// 에라토스테네스의 체 알고리즘 - 2의 배수, 3의 배수, 5의 배수, 7의 배수를 제외하면 남는 수는 소수이다.
// 1. boolean 배열을 true로 모두 초기화(true일때 소수임)
// 2. i를 2부터 시작하여 i * i 가 result의 크기보다 작을 때 까지 반복 - 배수를 제외하기 때문에 i * i 가 result보다 크면 의미 없음
private static void getEratosthenes(boolean[] isPrime) {
for (int i = 2; i * i < isPrime.length; i++) {
if (isPrime[i]) {
for (int j = i * i; j < isPrime.length; j += i) {
isPrime[j] = false;
}
}
}
}
private static void initEratosthenes(boolean[] isPrime) {
for (int i = 2; i < isPrime.length; i++) {
isPrime[i] = true;
}
}
}반응형
'Algorithm > Theory' 카테고리의 다른 글
| 유클리드 호제법 (1) | 2023.12.03 |
|---|---|
| [Java] 병합 정렬(Merge Sort) (0) | 2022.07.06 |
| [Java] Counting Sort(카운팅 정렬) (0) | 2022.05.07 |
| [자바] 셸 정렬(Shell Sort) (0) | 2022.01.27 |
| [자바] 단순 선택 정렬과 단순 삽입 정렬 (0) | 2022.01.22 |




댓글